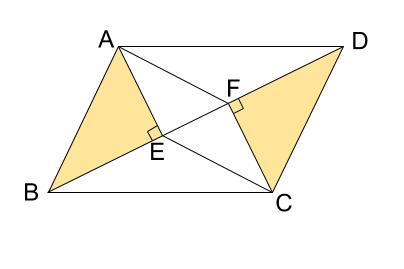
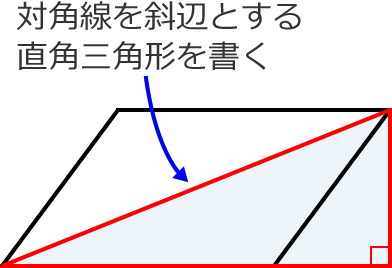
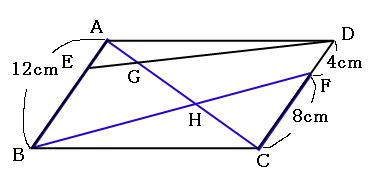
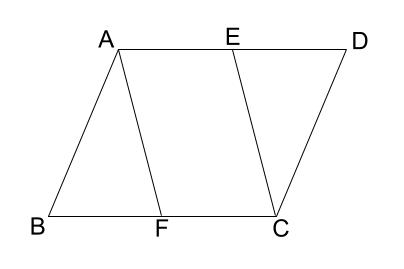
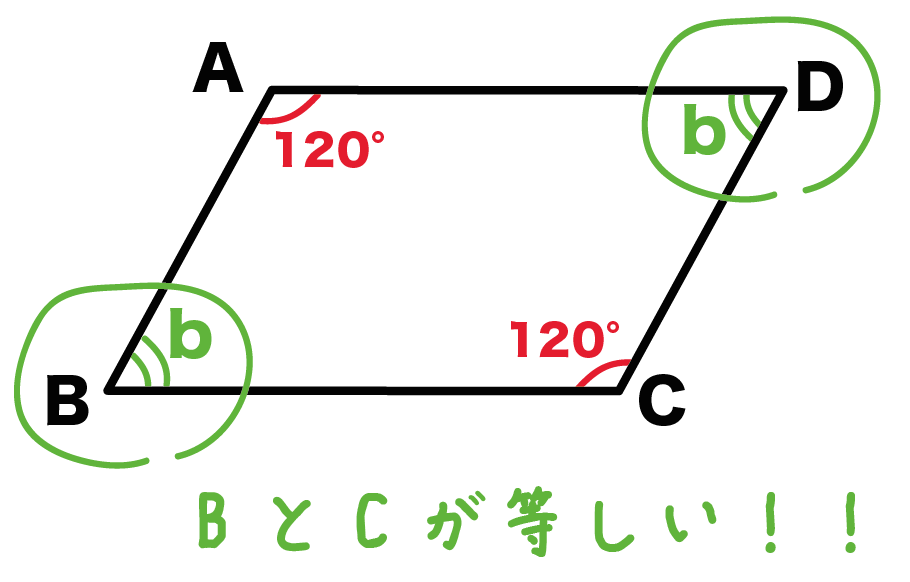
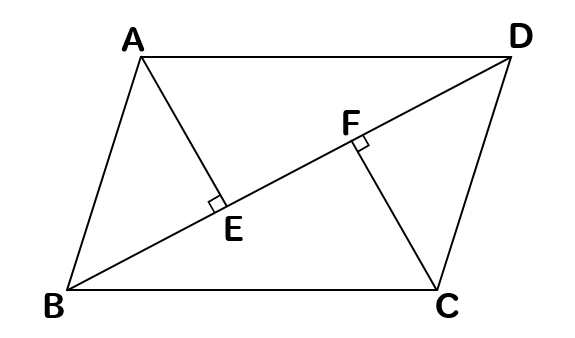
解説 垂線を引いて作られた四角形が平行四辺形であることを示す問題です。 当然ですが、この垂線の図形的性質から証明されるはずです。 垂直という角度の情報から、 AE//CF A E / / C F が言えます。 錯角が等しいので平行、ということです。 よって
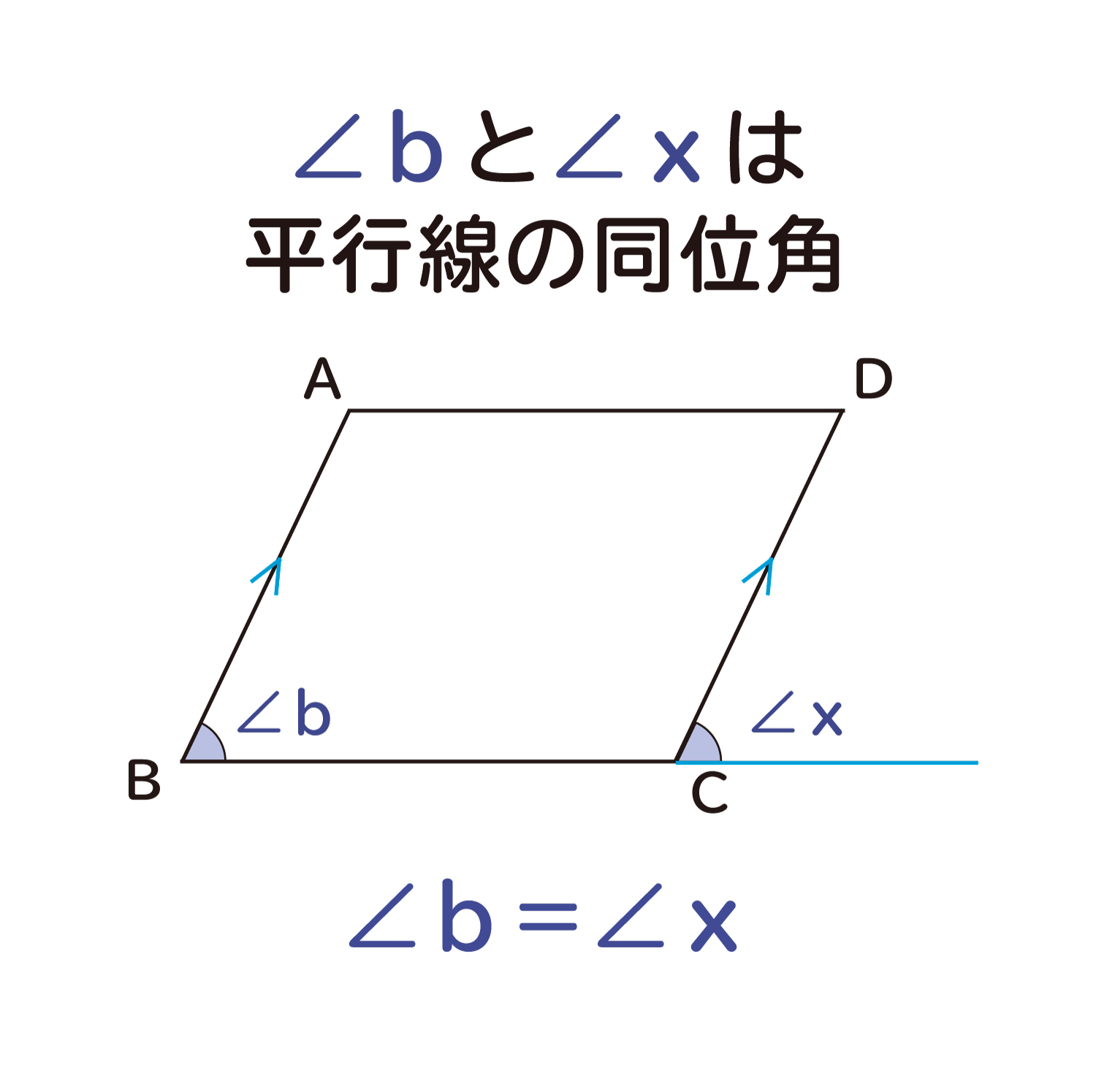
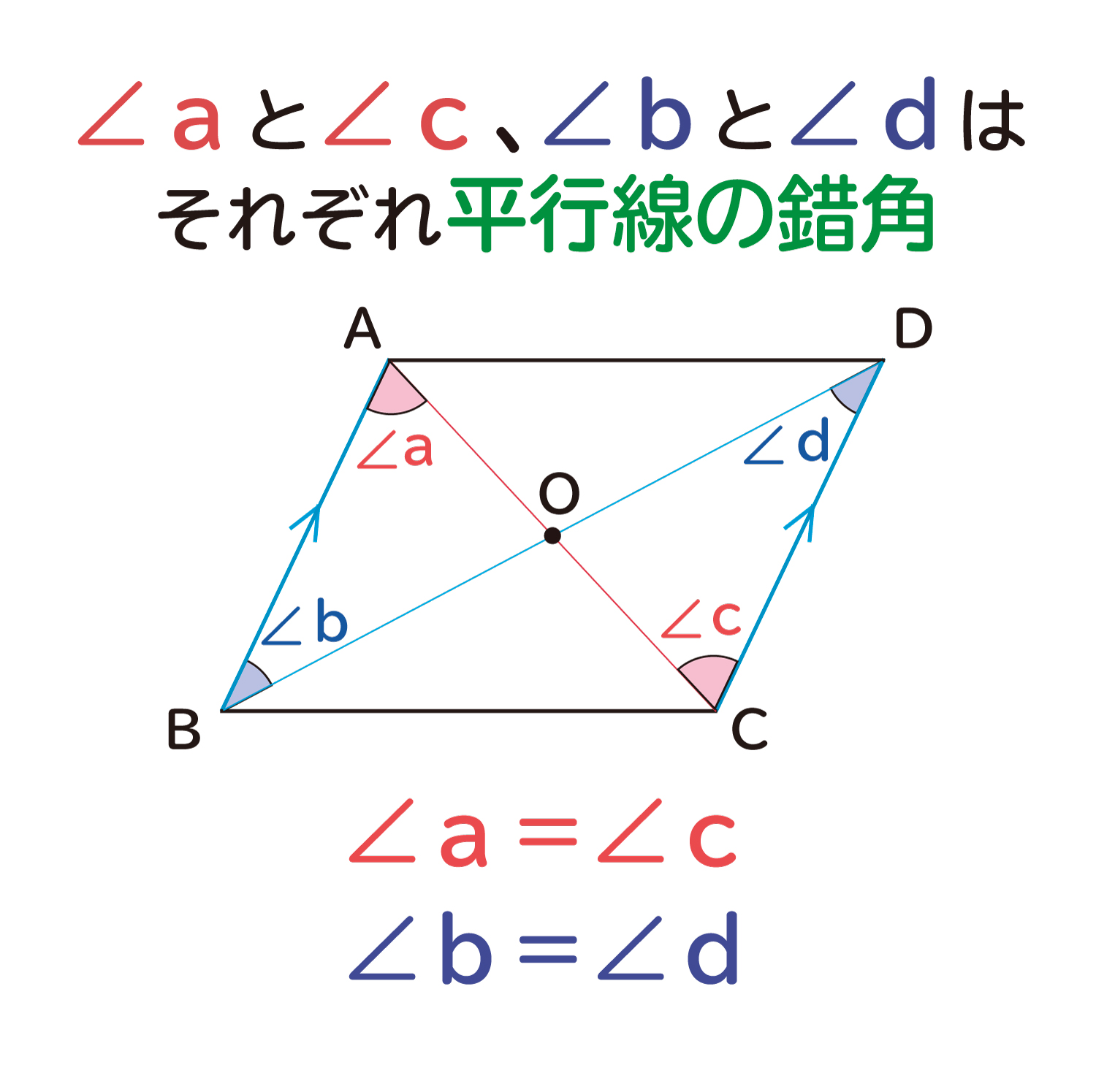
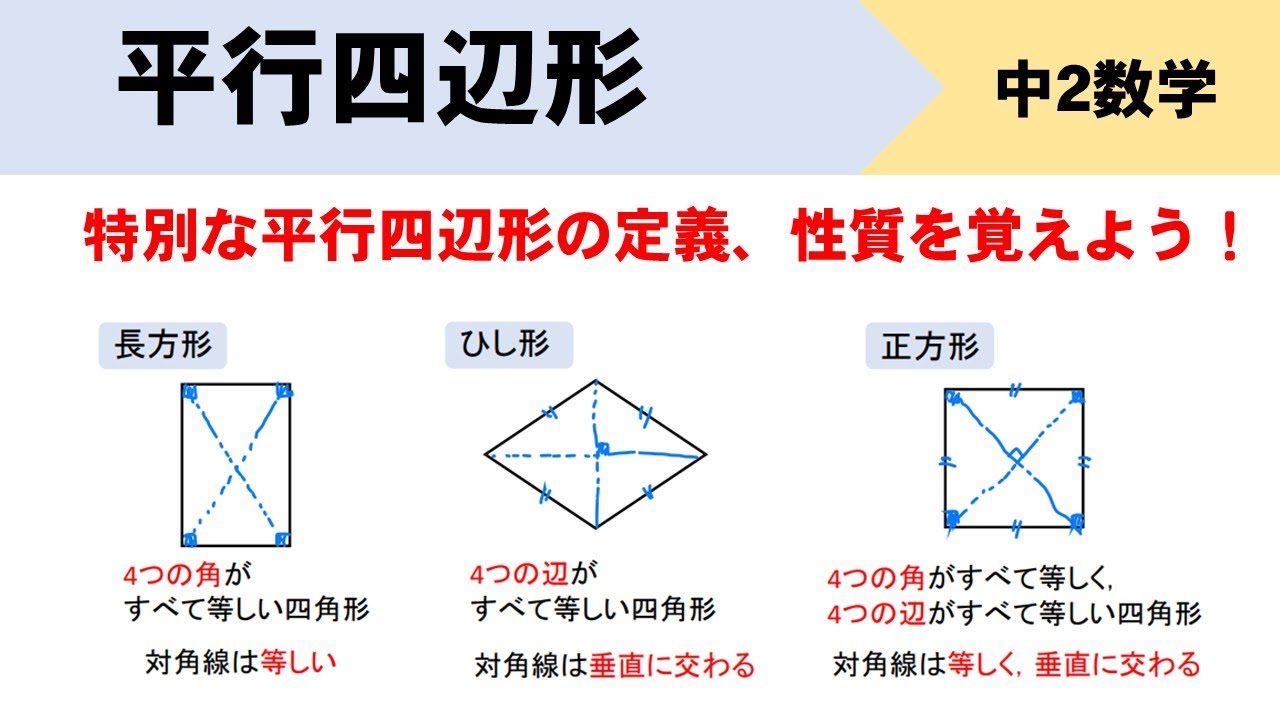
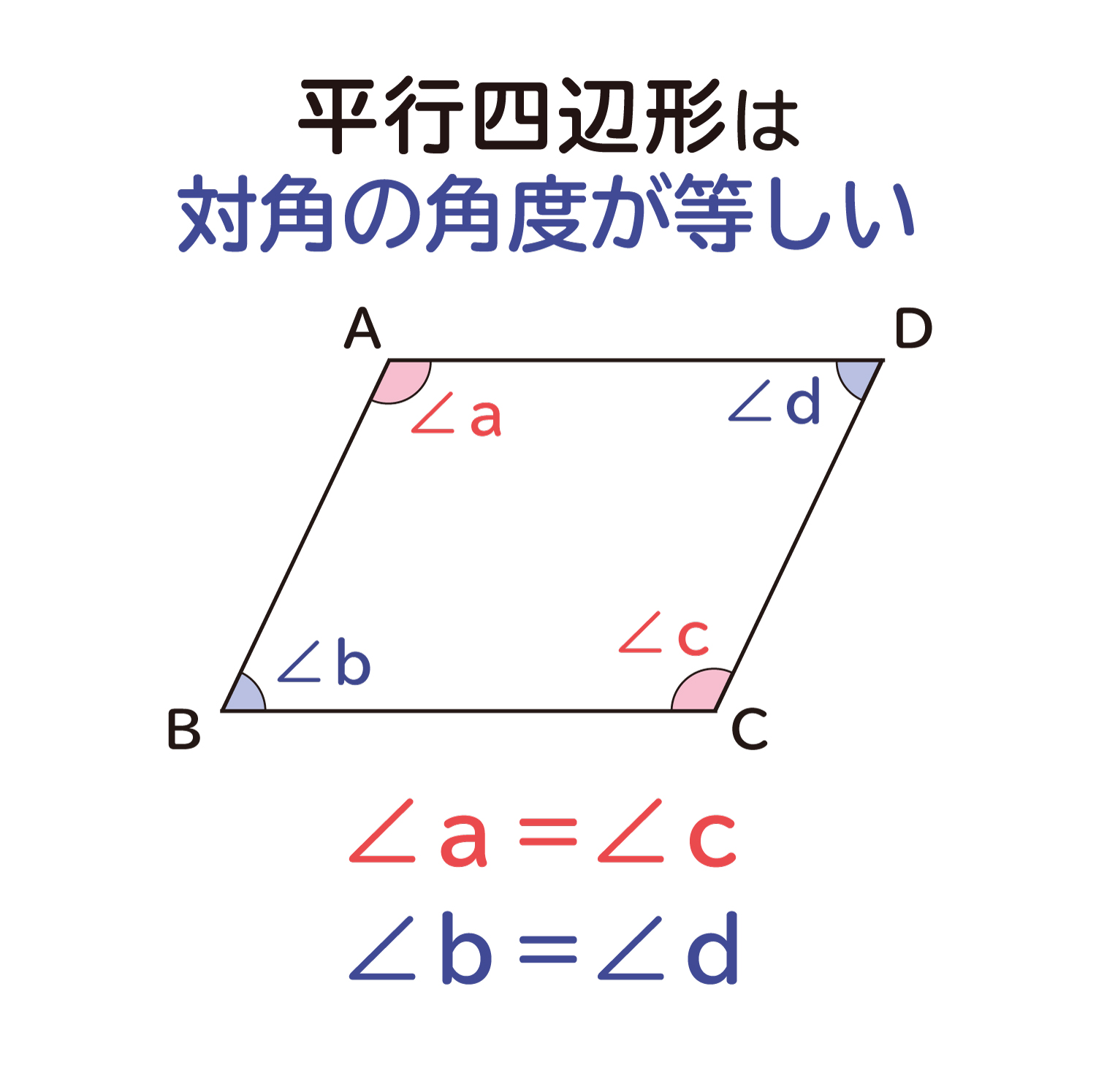
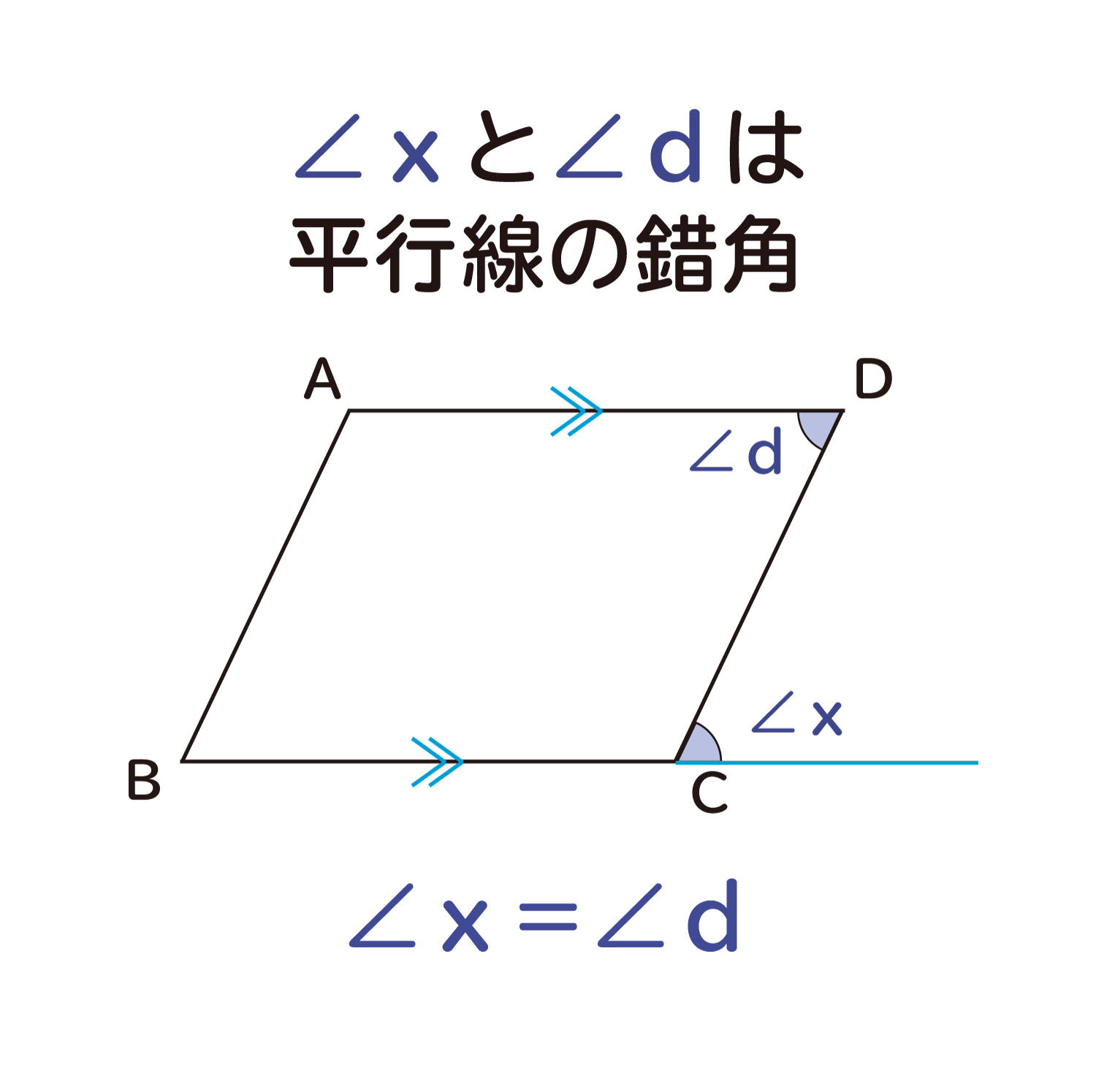
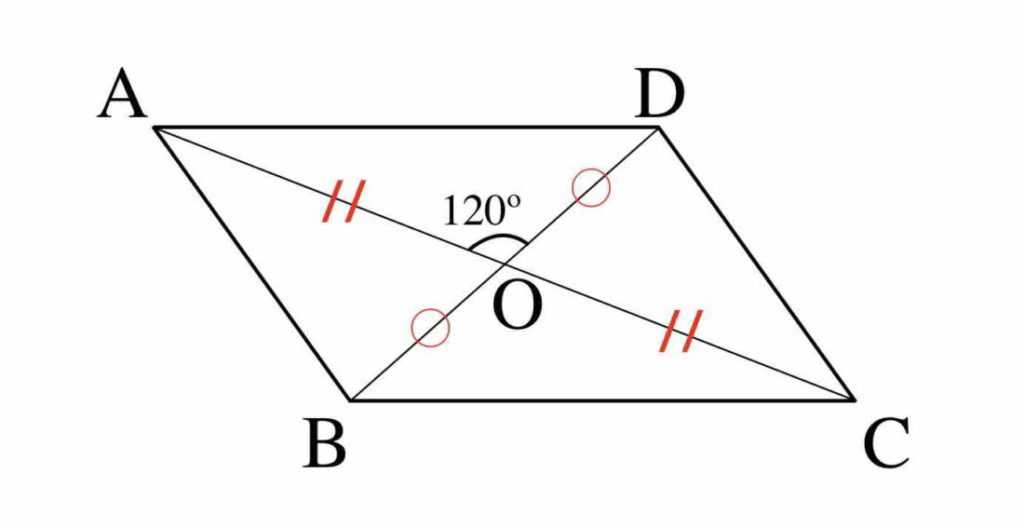
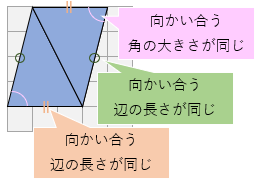
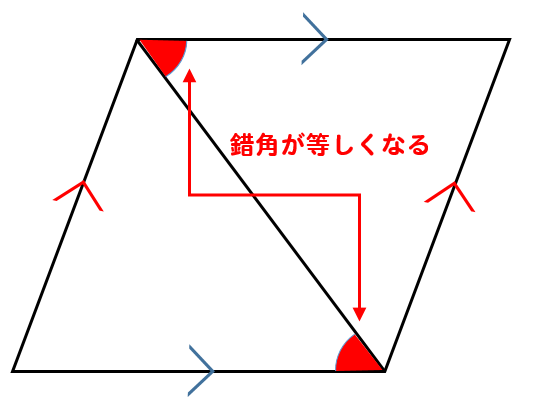
平行四辺形 対角線 角度-平行線の錯角は等しいので∠oab=∠ocd, ∠oba=∠odc 平行線の対辺は等しいので、ab=cd よって1組の辺とその両端の角がそれぞれ等しいので aob≡ cod 合同な図形の対応する辺は等しいのでao=co, bo=do よって平行四辺形の対角線はそれぞれの中点で交わる平行線と角の性質は、証明問題はもちろん普通に角度を求める問題でもかなり高い頻度で使います。 入試の図形問題を解くためには、理解必須の性質です。 平行四辺形の性質は、難しめの証明問題などで必要になることがあります。 平行線の角度の性質よりは重要度は下がりますが (個人の感想です)、もっと図形問題で確実に点数を取りたいなら、問題中で使える
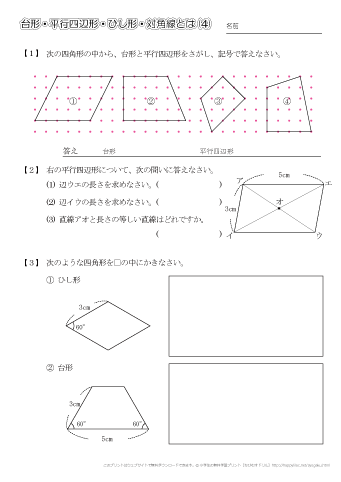
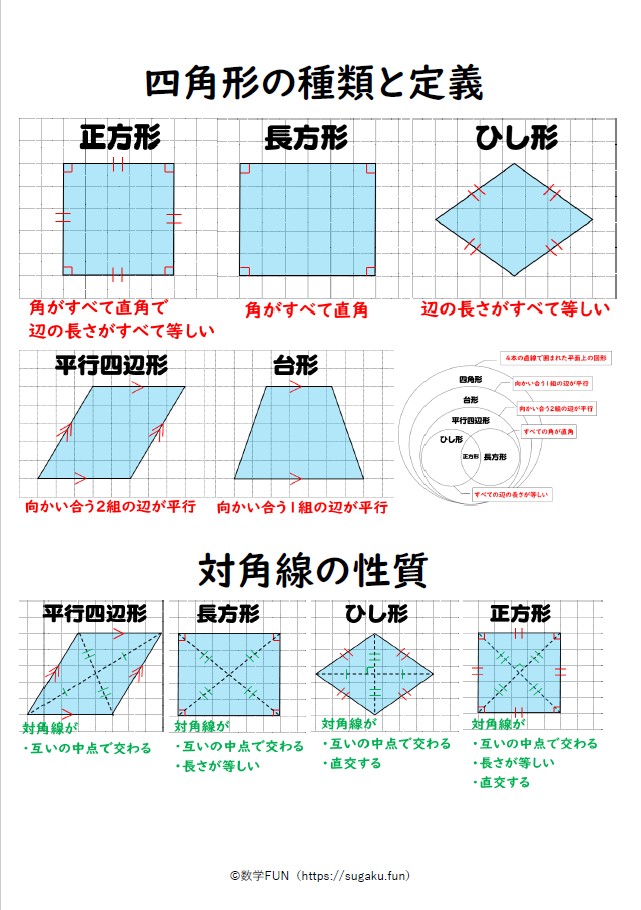
平行四辺形 対角線 角度のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  |  |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  | |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 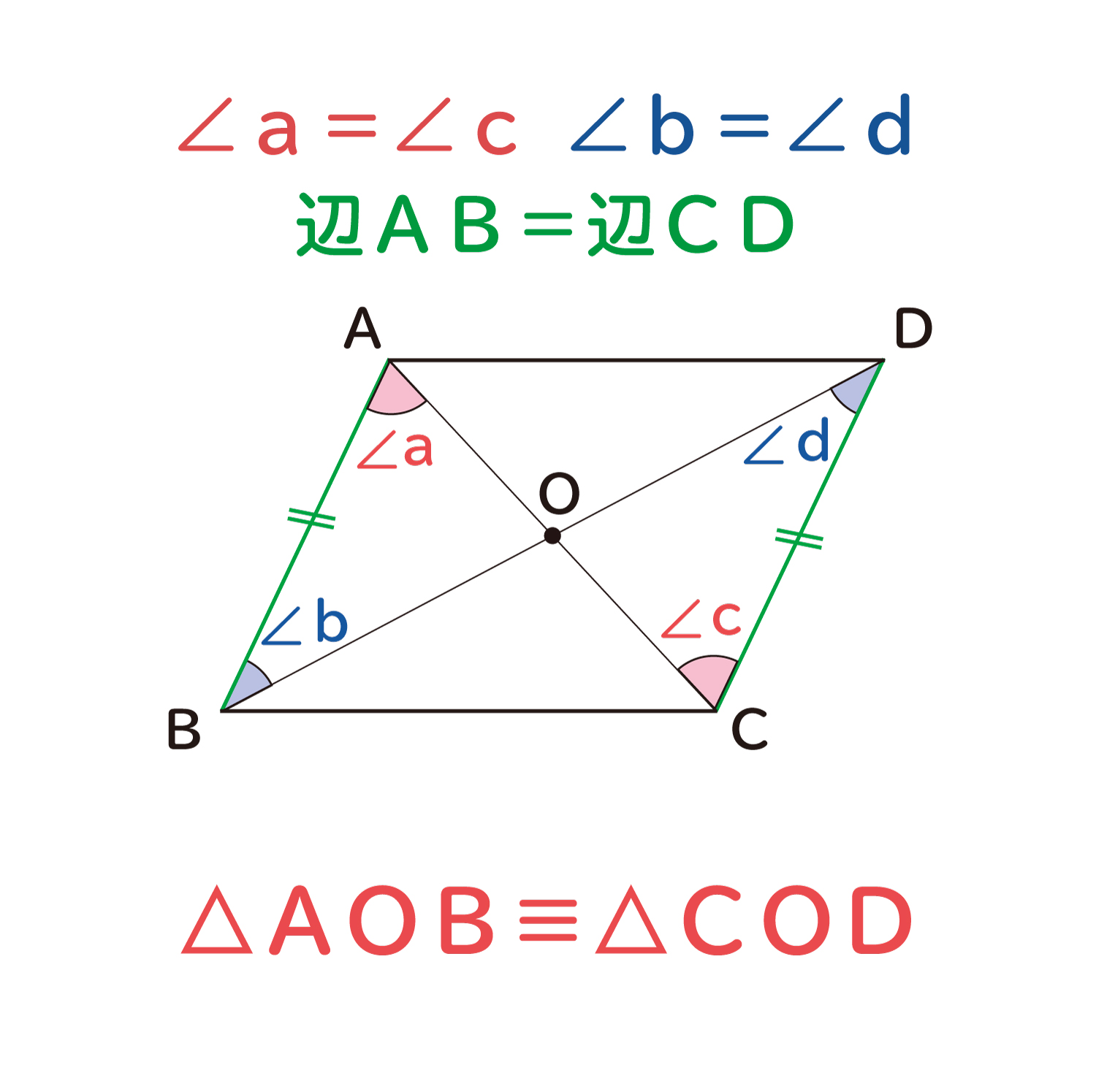 | |
 |  |  |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 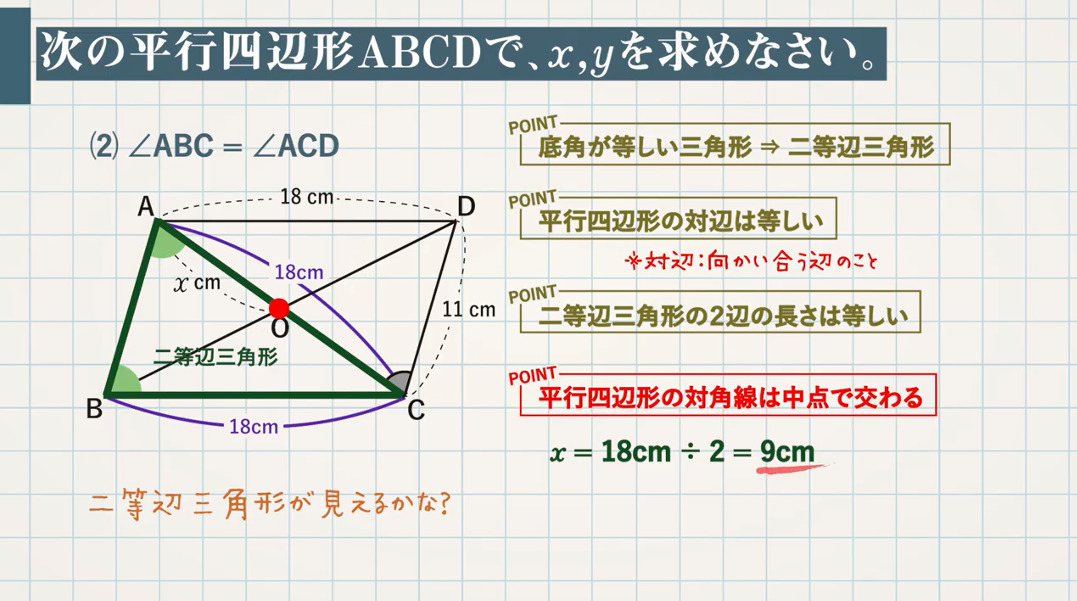 |  |
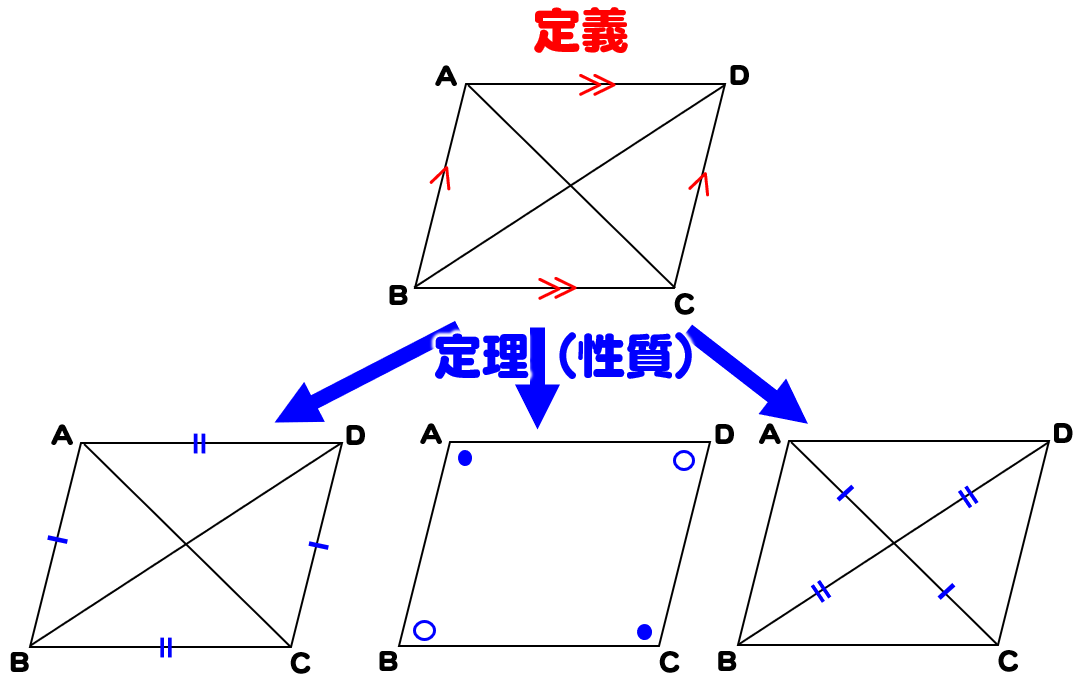 | ||
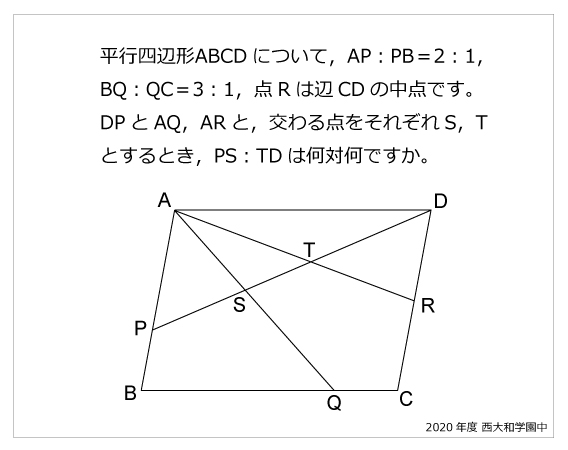 |  |  |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
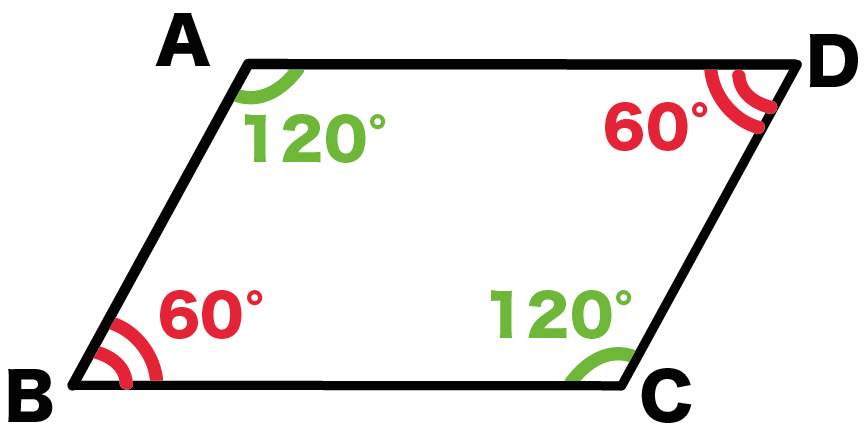 | 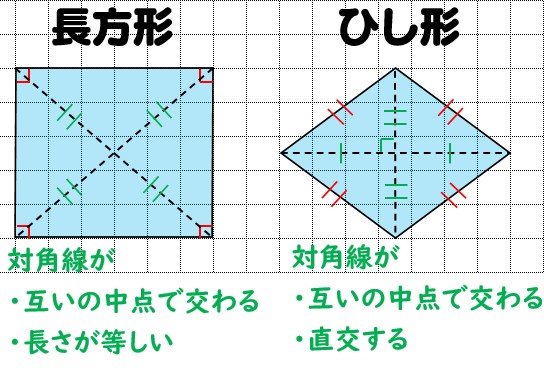 | 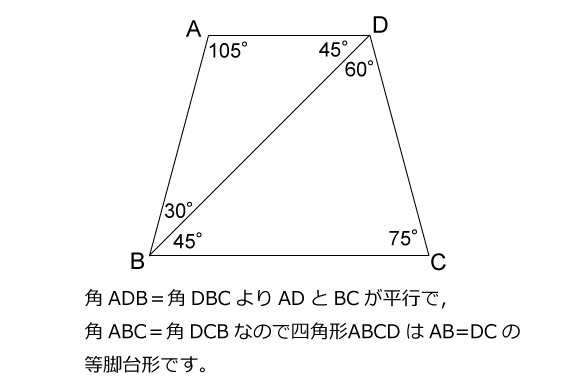 |
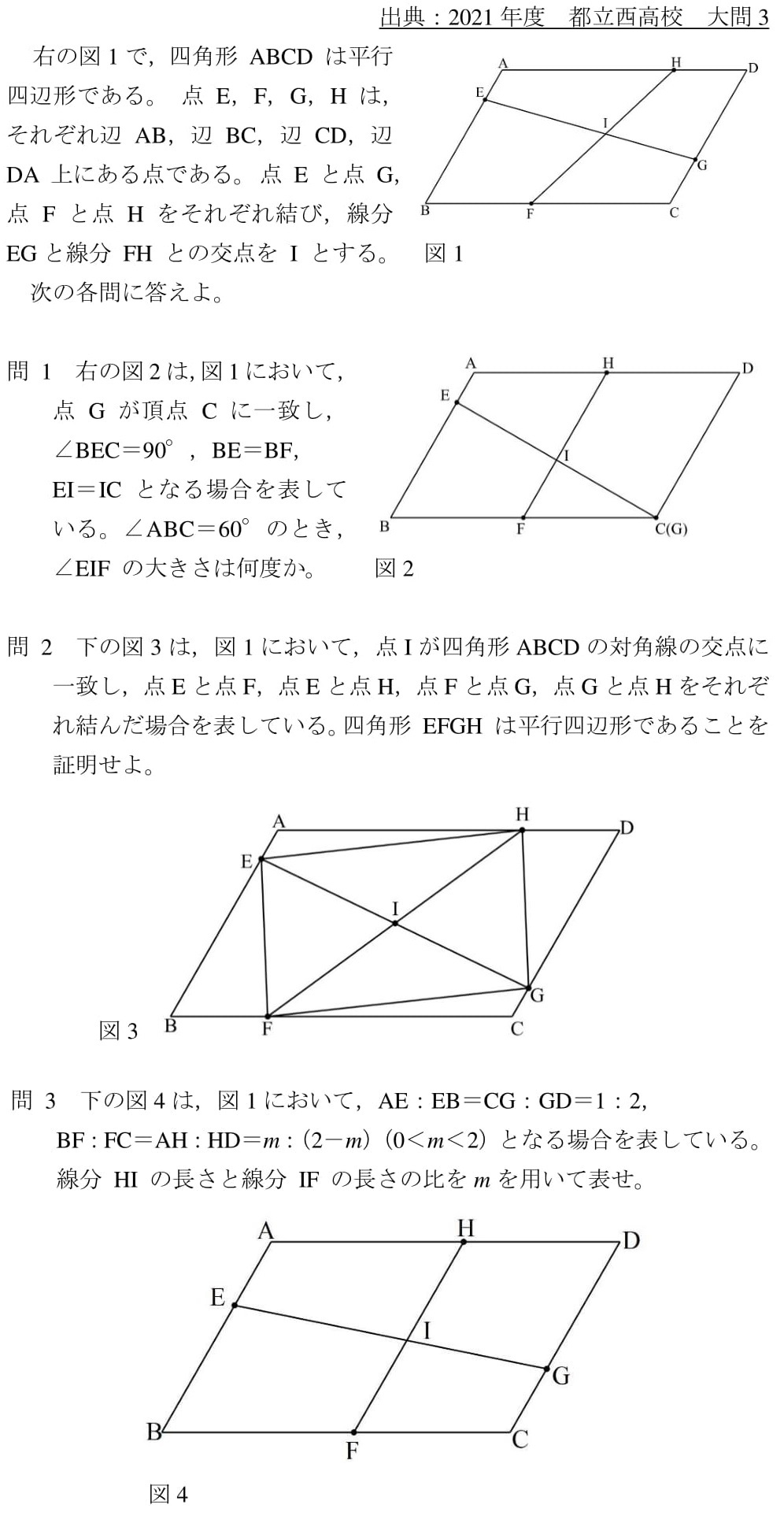 | ||
 |  |  |
 |  | |
「平行四辺形 対角線 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
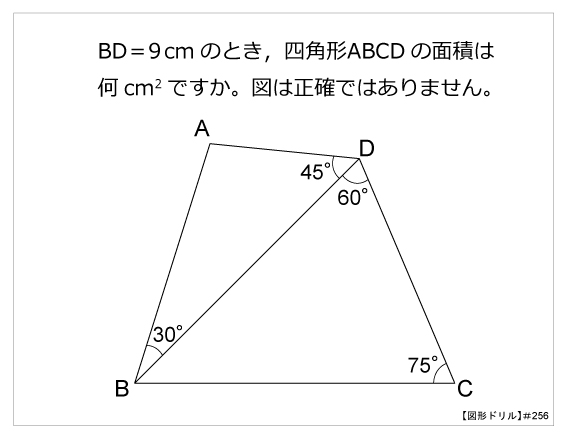
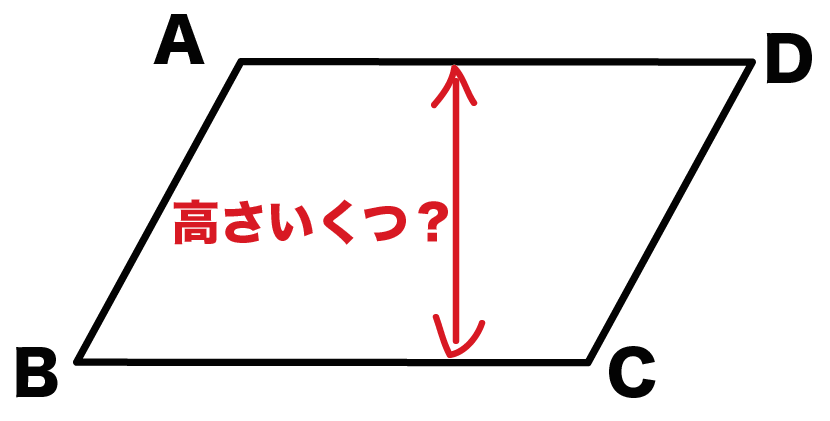
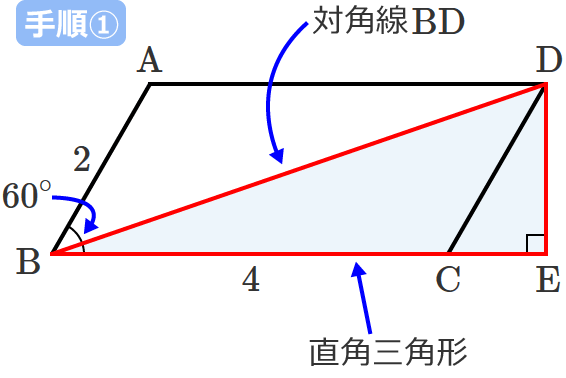
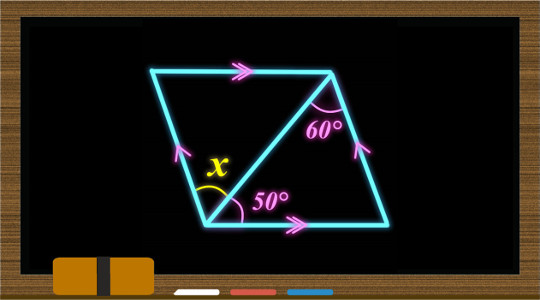
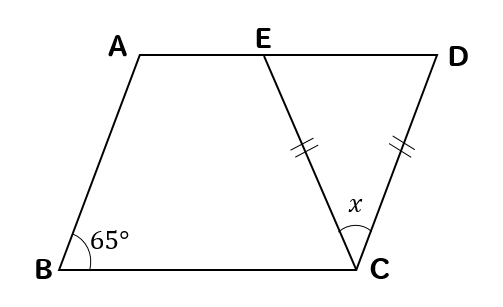
POINT:平行四辺形の対角は等しい $\rm ∠D=∠B=78°$ $\rm ∠CBE$( 1つ)$=78°÷2=39°$ 三角形の内角の和は $180°$ なので、 $\rm ∠BCE=180°90°39°=51°$ 平行線の錯角は等しいので、 $\rm ∠BCE=∠DAC$ よって、$x=\textcolor{red}{51°}$ 線分・三角形,平行四辺形の内部を表すベクトル方程式の演習です。 (例題1) 定三角形\(ABC\)がある。 実数\(k\)に対して、点\(P\)が \(\overrightarrow{PA}2\overri 線分・三角形,平行四辺形の内部を表すベクトル方程式の演習です。
Incoming Term: 平行四辺形 対角線 角度, 平行四辺形 対角線 角度 二等分, 平行四辺形 対角線 角度 求め方, 平行四辺形 対角線 角度 半分,




0 件のコメント:
コメントを投稿